Derivative Of Inverse Trig - Unraveling The Basics And Applications
Derivative of inverse trig is a cornerstone concept in calculus that bridges the gap between trigonometry and advanced mathematical thinking. When you're diving into calculus, it's crucial to understand how inverse trigonometric functions behave when differentiated. These functions aren't just abstract mathematical constructs; they're practical tools used across a variety of scientific and engineering disciplines. They allow you to analyze the behavior of angles and their relationships with sides in triangles, making them indispensable in fields like physics, engineering, and even architecture.
Understanding the derivative of inverse trig functions can seem a bit tricky at first glance, but with the right approach, it becomes much simpler. Think of these derivatives as a way to measure how quickly the angle changes with respect to its trigonometric value. By grasping this concept, you'll be better equipped to tackle problems involving rates of change, motion, and optimization. These derivatives are also key players in integration, which is a fundamental part of calculus.
Before we move forward, it's worth noting that inverse trig derivatives are more than just formulas to memorize. They carry significant meaning and reveal intriguing patterns in mathematics. As we explore these derivatives, you'll see how their algebraic nature contrasts with the trigonometric functions they're derived from. So, let's get started and uncover the fascinating world of inverse trig derivatives!
Table of Contents
- What is the Derivative of Inverse Trig?
- Why Are Derivatives of Inverse Trig Important?
- How to Calculate the Derivative of Inverse Trig?
- What Are the Common Inverse Trig Functions?
- Derivative of Inverse Trig - Practical Examples
- How Does the Chain Rule Apply to Derivative of Inverse Trig?
- Can You Solve Real-World Problems Using Derivative of Inverse Trig?
- Summary of Derivative of Inverse Trig
What is the Derivative of Inverse Trig?
Let's start with the basics. When you're talking about the derivative of inverse trig, you're essentially discussing how quickly the angle changes in relation to its trigonometric value. For instance, the inverse sine function, also known as arcsine, has a derivative that measures this rate of change. It's important to recognize that these derivatives aren't just random formulas; they have a logical structure that ties back to the properties of trigonometric functions.
For example, take a look at the formula for the derivative of arcsine: \( \dfrac{d}{dx} (\arcsin(x)) = \dfrac{1}{\sqrt{1-x^2}} \). This expression reveals how the rate of change varies depending on the input value. Notice how the denominator involves a square root? That's a common feature in many inverse trig derivatives, and it reflects the geometric constraints of the underlying trigonometric functions.
Why Are Derivatives of Inverse Trig Important?
Alright, so why do we even care about the derivative of inverse trig? Well, these derivatives play a critical role in calculus, particularly when it comes to integration. They allow us to solve problems that involve finding areas, volumes, and other quantities that change over time. Plus, they're incredibly useful in physics and engineering, where angles and their relationships are often key factors in problem-solving.
Let’s take a practical example. Imagine you're designing a bridge and need to calculate the optimal angle for the supports. The derivative of an inverse trig function could help you determine how small changes in the angle affect the overall stability of the structure. This kind of insight is invaluable in real-world applications.
How to Calculate the Derivative of Inverse Trig?
Calculating the derivative of inverse trig functions might seem challenging, but it's really just about following a few straightforward steps. First, identify the function you're working with, whether it's arcsine, arccosine, or arctangent. Then, apply the appropriate formula for its derivative. For example, the derivative of arctangent is \( \dfrac{d}{dx} (\arctan(x)) = \dfrac{1}{1+x^2} \).
One trick to make this process easier is to remember that these derivatives often involve square roots or fractions. So, if you're stuck, look for patterns in the formula that resemble these structures. Sometimes, just a little observation can make all the difference.
What Are the Common Inverse Trig Functions?
Before we delve deeper into the derivatives, let's review the common inverse trig functions. These include arcsine, arccosine, arctangent, arcsecant, arccosecant, and arccotangent. Each function corresponds to a specific trigonometric function and its inverse relationship. For instance, arcsine is the inverse of sine, meaning it gives you the angle whose sine is a particular value.
One interesting thing to note is that these functions are defined only within certain domains. For example, arcsine is only valid for values between -1 and 1. This restriction is necessary to ensure that each input corresponds to a unique output, which is a requirement for inverse functions.
Derivative of Inverse Trig - Practical Examples
Let’s look at some practical examples to see how the derivative of inverse trig works in action. Suppose you're given the function \( f(x) = \arccos(x) \). To find its derivative, you'd use the formula \( \dfrac{d}{dx} (\arccos(x)) = -\dfrac{1}{\sqrt{1-x^2}} \). Notice the negative sign? That indicates the function is decreasing as \( x \) increases, which aligns with the behavior of the cosine function.
Another example involves the arctangent function. If \( g(x) = \arctan(x) \), then \( \dfrac{d}{dx} (\arctan(x)) = \dfrac{1}{1+x^2} \). Here, the derivative is always positive, reflecting the fact that the arctangent function increases as \( x \) increases. These examples illustrate how the derivatives of inverse trig functions provide valuable insights into their behavior.
How Does the Chain Rule Apply to Derivative of Inverse Trig?
The chain rule is a powerful tool in calculus, and it applies just as well to the derivative of inverse trig functions. Essentially, the chain rule allows you to differentiate composite functions by considering the inner and outer functions separately. For example, if you have \( h(x) = \arcsin(2x) \), you'd first differentiate the outer function \( \arcsin(u) \) and then multiply by the derivative of the inner function \( u = 2x \).
Applying this approach, the derivative becomes \( \dfrac{d}{dx} (\arcsin(2x)) = \dfrac{2}{\sqrt{1-(2x)^2}} \). This shows how the chain rule simplifies the process of differentiating more complex inverse trig expressions. By breaking the problem into smaller parts, you can tackle even the most intricate derivatives with confidence.
Can You Solve Real-World Problems Using Derivative of Inverse Trig?
Absolutely! The derivative of inverse trig functions finds applications in numerous real-world scenarios. For example, in physics, they're used to calculate angular velocities and accelerations. In engineering, they help determine optimal angles for structures and mechanisms. Even in navigation, these derivatives assist in calculating distances and directions based on angles.
Consider a scenario where you're analyzing the motion of a pendulum. The angle of the pendulum's swing can be modeled using an inverse trig function, and its rate of change corresponds to the derivative. By understanding this relationship, you can predict how the pendulum's motion evolves over time and adjust parameters to achieve desired outcomes.
Summary of Derivative of Inverse Trig
So, we've covered a lot of ground when it comes to the derivative of inverse trig functions. From the basics of what these derivatives represent to their practical applications, you now have a solid foundation to build upon. Remember, these derivatives aren't just abstract formulas; they're practical tools that reveal the dynamic relationships between angles and their trigonometric values.
As you continue your studies in calculus, keep in mind that the derivative of inverse trig functions will prove to be a valuable asset. Whether you're solving complex equations or tackling real-world problems, these derivatives offer insights and solutions that are both elegant and effective. So, take some time to practice and familiarize yourself with these concepts, and you'll be well on your way to mastering this essential part of calculus.
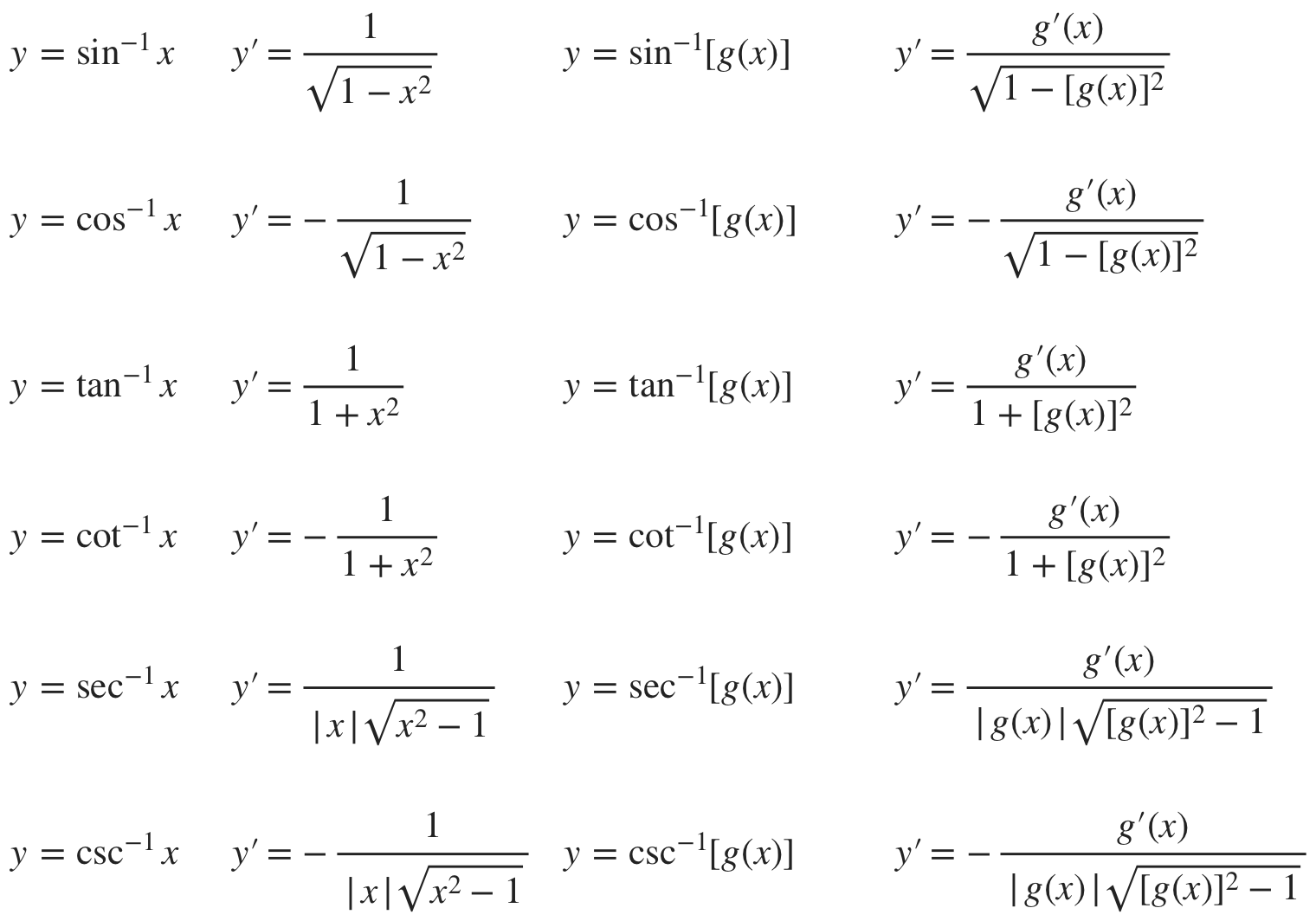
Finding inverse trig derivatives — Krista King Math | Online math help

PPT - 3.8 Derivatives of Inverse Trigonometric Functions PowerPoint

PPT - Aim: How do we differentiate Inverse Trig functions? PowerPoint