How To Calculate Variance - A Simple Guide For Everyone
Are you looking for a straightforward way to understand how to calculate variance? Well, you’ve come to the right place. Variance is a statistical concept that helps us understand how much numbers in a dataset differ from the average. It’s like measuring how far apart your favorite fruits are from the "fruit basket average." Whether you’re a student, a professional, or just someone curious about numbers, variance plays a big role in decision-making and data analysis. This guide will walk you through everything you need to know about calculating variance.
So, why is variance important? Imagine you’re trying to decide whether a certain stock is stable or not. By calculating the variance of its daily price changes, you can figure out how much the prices fluctuate. A high variance might mean the stock is risky, while a low variance suggests it’s more consistent. Understanding variance gives you insight into the behavior of data, making it a valuable tool in fields like finance, quality control, and risk management. It’s not just about numbers; it’s about understanding patterns.
Before we jump into the details, let’s clarify something. Variance is often confused with standard deviation, but they’re different. Variance measures how spread out numbers are, while standard deviation gives you a sense of how far individual numbers are from the mean. Both are useful, but variance tends to be more foundational. In fact, most of the time, people calculate variance to eventually find the standard deviation. But don’t worry, we’ll cover all of this and more in a way that’s easy to follow. Now, let’s get started!
What Exactly is Variance?
Alright, let’s break it down. Variance is basically the average of the squared differences from the mean. It’s a way to quantify how much the numbers in a dataset vary from the average. For example, if you’re measuring the heights of a group of people, variance will tell you how much each person’s height differs from the group’s average height. It’s a simple concept, but it holds a lot of power when it comes to analyzing data.
Why Should You Care About Variance?
Here’s the deal: variance gives you a clearer picture of your data. It’s like taking a blurry photo and sharpening it. By calculating variance, you can identify patterns, spot outliers, and make better decisions. Let’s say you’re a teacher trying to understand how well your students performed on a test. Variance can help you see if most students scored close to the average or if there was a wide range of scores. It’s a tool that helps you make sense of the world around you, one number at a time.
How to Calculate Variance - Step by Step
Now, let’s talk about how to calculate variance. It’s simpler than it sounds. First, you need to find the mean of your dataset. Add up all the numbers and divide by how many there are. Next, subtract the mean from each number to find the difference. Then, square each of those differences. Why square them? Because squaring gets rid of negative numbers, which makes the math easier. Finally, add up all the squared differences and divide by the number of data points. That’s it!
How to Calculate Variance for Population Data?
When you’re working with population data, the process is similar, but there’s a small difference. Instead of dividing by the number of data points, you divide by the total population size. This gives you a more accurate measure of variance because you’re accounting for every single data point in the population. For instance, if you’re analyzing the heights of all students in a school, you’d use population variance to get the most precise result.
What’s the Difference Between Population and Sample Variance?
Let’s say you’re conducting a survey but can’t collect data from everyone. In that case, you use sample variance. Sample variance is calculated slightly differently. Instead of dividing by the number of data points, you divide by one less than the number of data points. This adjustment, called Bessel’s correction, gives you a better estimate of the population variance. It’s like trying to guess the average height of all students in a school by only measuring a few of them.
How to Calculate Variance for Sample Data?
For sample data, the steps are mostly the same. Find the mean, subtract it from each data point, square the differences, add them up, and divide by one less than the number of data points. It’s a bit tricky at first, but once you get the hang of it, it becomes second nature. Think of it like learning to ride a bike. At first, it’s wobbly, but soon enough, you’re cruising down the street.
How to Calculate Variance Using a Calculator?
If you’re not a fan of doing all the math by hand, there’s good news. You can use a calculator or an online tool to calculate variance. Just input your data, and the calculator will do the rest. It’s quick, easy, and accurate. Plus, most calculators will also give you other useful stats, like the mean, standard deviation, and sum of squares. It’s like having a personal assistant for all your math needs.
Can You Really Trust Variance?
That’s a great question. Variance is a reliable measure, but it’s not perfect. One downside is that it’s expressed in squared units, which can be a bit confusing. For example, if you’re measuring heights in inches, the variance will be in square inches. That’s why people often use standard deviation, which is in the same units as the original data. Still, variance is a solid starting point for understanding how spread out your data is.
How to Calculate Percent Variance?
Percent variance is a bit different. It measures how much a value has changed in percentage terms. To calculate it, subtract the planned value from the actual value, divide by the planned value, and multiply by 100. For example, if you planned to sell 100 units but sold 120, the percent variance would be 20%. It’s a handy tool for tracking performance and identifying areas for improvement.
What Are the Types of Variance?
There are two main types of variance: population variance and sample variance. Population variance is used when you have data for the entire population, while sample variance is used when you only have a portion of the data. Both are important, but they’re calculated slightly differently. It’s like choosing between a full recipe and a quick version. Each has its own purpose and application.
Is Variance Always Useful?
In some respects, variance isn’t used as much on its own. It’s often a stepping stone to calculating standard deviation, which is more commonly used. However, variance still has its place. It’s a foundational concept that helps you understand the variability in your data. Without variance, it would be much harder to make sense of the world around you. So, while it might not always be the star of the show, it’s definitely a key player.
Final Thoughts
In short, learning how to calculate variance is a valuable skill that opens up a world of possibilities. Whether you’re analyzing stock prices, student test scores, or product quality, variance gives you the tools you need to make informed decisions. By following the steps we’ve outlined and using the right tools, you can calculate variance with confidence. So, go ahead and give it a try. You might be surprised at how much you can learn from a little bit of math.

Variance Calculator (with Steps) - Inch Calculator
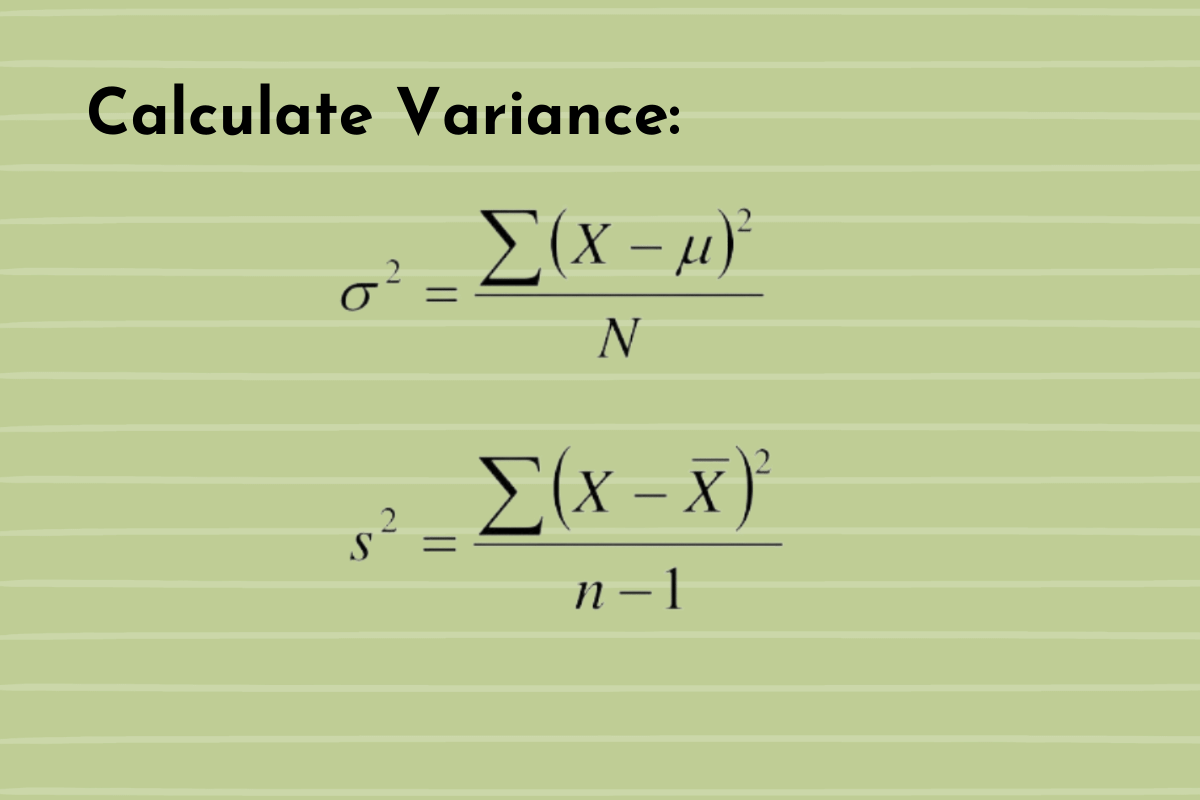
How to Calculate Variance | knowhowadda
Variance Formula Probability